Ein wenig Corona-Mathematik
Montag, 30.03.2020
Die Diskussion um die Maßnahmen gegen das Corona-Virus SARS-CoV-2 werden sehr hitzig geführt. Dabei lässt sich der Verlauf der Pandemie mit relativ einfachen Formeln modellieren. Das ist hilfreich für eine sachliche Diskussion.
Von Infektionen und Zahlenreihen
Die Diskussion scheint sich in zwei Lager zu polarisieren. Den einen kann es nicht schnell genug gehen, restriktive Maßnahmen zur Eindämmung der Virusausbreitung zu etablieren. Die anderen halten das ganze Szenario für eine Massenhysterie, wenn nicht gar für eine gezielte Verschwörung bestimmter kapitalistischer oder kontrollbegieriger Kreise. Die Auseinandersetzung ist so hitzig, dass sie zum Beispiel zu folgendem Zitat in der taz führt:
„Die Christian Drostens der Republik haben schon früh gewarnt, dass die Zunahme der Corona-Infektionen exponentiell und nicht linear ist: Wenn jeder Infizierte nur zwei Menschen ansteckt, dann geht die Kette so: 1, 2, 4, 8, 16, 32, 64, 128, 256 – und so weiter.“
Felix von Leitner hat in seinem Blog die Aussage bereits seziert. Daraufhin haben ihm Leser geschrieben, mit der Zahlenreihe seien nur die Neuinfektionen gemeint, nicht die absoluten Fallzahlen. Deshalb würden die Zahlen doch stimmen. Das hat dann letztlich den Anstoß gegeben, diesen Artikel zu schreiben.
Lassen Sie uns das kurz einmal nachrechnen. Ich verspreche, dass das ganz einfach wird. Sie können zum Nachvollziehen Excel oder ein anderes Tabellenkalkulationsprogramm benutzen. In die erste Zelle A1 schreiben wir den Wert 1, von dem alles ausgeht. In Zelle B2 schreiben wir =A1*2. Das sind die Neuansteckungen von Zelle A1. Links daneben in die Zelle A2 schreiben wir =A1+B2. Das ist die neue Gesamtzahl aller Fälle. Dann sieht das ganze so aus:
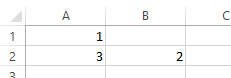
Und nun können wir das schöne Werkzeug von Excel benutzen, mit dem man Formeln auf andere Zellen übertragen kann. Dazu wählen wir die beiden Zellen A2,B2 an und ziehen mit der Maus das kleine grüne Quadrat rechts unten nach unten:
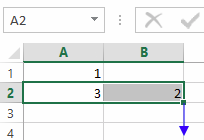
Damit sieht die Tabelle so aus:
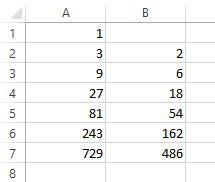
Dann würde die Zahlenfolge in der taz in keinem Fall stimmen. Richtig?
Nein. Ich bin erst einmal in die gleiche Falle getappt.
Die Berechnungen gehen von einer sogenannten Basisreproduktionszahl R0 aus. R0 gibt an, wie viele Menschen eine infizierte Person durchschnittlich ansteckt, und zwar ohne die Einflüsse zu berücksichtigen, die die Ausbreitung dämpfen könnten, wie Immunität (natürlich und durch Impfung), Medikation oder soziale Maßnahmen.
R0 gibt an, wie viele Menschen eine infizierte Person durchschnittlich ansteckt – und zwar insgesamt. R0 ist kein "Zinsfaktor", bei dem Zinseszins entsteht. Die Neuinfektionen In der gegenwärtigen Generation stecken R0 * In Personen an und diese müssen zum Bestand der gegenwärtigen Generation addiert werden. Wir müssen in unsere Tabelle in Zelle B3 also eine neue Formel schreiben, das ist B2 * 2. Damit ergibt sich folgender Verlauf der Tabelle:
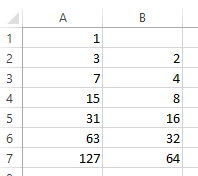
In Spalte A stehen die Gesamtinfektionen der jeweiligen Generation und in Spalte B die jeweils neu hinzugekommenen.
Die Exponentialfunktion
Es wird in Bezug auf Corona ja immer von der Exponentialfunktion gesprochen, es wird also Zeit, zu erklären, was das überhaupt ist. Eine Exponentialfunktion zeichnet sich durch folgende Formel aus:
y = bx
oder, um es in Excel-Schreibweise darzustellen:
y = b ^ x
wobei b die „Basis“ genannt wird.
Die von der taz gezeigte Zahlenreihe entspricht übrigens der Funktion
y = 2 ^ x
für alle natürlichen Zahlen, also 0,1,2...
Man kann auch sagen: Mit jeder Generation wird y um den Faktor b größer.
Exponentialfunktionen als Geraden
Oft werden Exponentialfunktionen auf einer logarithmischen Skala angezeigt. Das hat den Vorteil, dass sie dann als Geraden erscheinen. Das kann man leicht zeigen. Der Logarithmus ist nämlich die Umkehrfunktion der Exponentialfunktion. Man kann also sagen:
log(10x) = x
Des weiteren kann man bx auch als 10 log(b)*x schreiben.
Gemäß der Formel log(10x) = x können wir daher sagen:
log(y) = log(b)*x
Vielleicht erinnern Sie sich noch an die Geradengleichungen in der Schule. Die obenstehende Formel kann als Gerade mit der Steigung log(b) dargestellt werden. Das ist höchst elegant. Immer, wenn die Berechnung mit Exponentialfunktionen etwas unhandlich wird, können wir beide Seiten einer Gleichung logarithmieren und können dann mit den simplen Geradengleichungen arbeiten. Das wird uns im folgenden noch hilfreich sein.
Gesamtzahl der Infektionen
Das Kapitel können Sie eigentlich überspringen (weiter bei: "Der praktische Einsatz"), da in der Epidemiologie immer nur mit den neu hinzugekommenen Infektionen gerechnet wird. Die Betrachtung ist nur für die Personen interessant, die sich ein Bild davon machen möchten, wie es möglich ist, für Werte von R < 1 eine Verdoppelungszeit zu berechnen. Dafür muss man dann die Gesamtzahl der Infektionen heranziehen.
Aus dem vorangegangenen Text und ein paar weiterführende Gedanken, die ich hier auslasse, ergibt sich, dass sich die Gesamtinfektionen zum Zeitpunkt einer Generation bei ungehinderter Ausbreitung so berechnet:
In = R0n-1 + R0n
Wobei n die Generation ist. Kann man das auf eine einfachere exponentielle Formel bringen?
Die Antwort ist: Nur näherungsweise. Für R0 = 2 gibt es dabei einen Sonderweg:
In = R0n+1 - 1
Schauen wir uns doch einmal in einem Diagramm den Unterschied der zwei Funktionen
R0n-1 + R0n (Gesamtinfektionen) und R0n (Neuinfektionen) an:
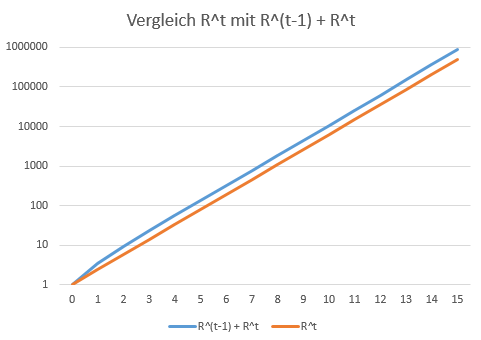
Anmerkung: Die Darstellung ist logarithmiert, eine Gerade ist in Wirklichkeit eine Exponentialfunktion. Was ich im Text n nenne, ist in der Grafik t. Die Bedeutung der beiden Symbole ist gleich.
Die blaue Kurve verläuft weitestgehend parallel zu der braunen Kurve. In Wirklichkeit schmiegt sie sich einer parallelen Geraden zu unserer Exponentialfunktion an, ohne sie je zu erreichen.
Wollte man nun eine Funktion angeben, um wieviel die blaue Kurve höher liegt, als die braune, also praktisch einen Faktor angeben, so ist dieser Faktor nicht konstant und seine Funktion über die Zeit nicht weniger komplex als die Addition R0n-1 + R0n.
Der praktische Einsatz
Wir haben gezeigt, dass ein exponentieller Verlauf entsteht, wenn wir davon ausgehen, dass eine Person im Schnitt R weitere Personen ansteckt, wobei R die Reproduktionszahl bzw. Reproduktionsrate ist. R = R0, wenn es keine hemmenden Faktoren der Ausbreitung gibt. Und wir wissen nun, wie wir die Anzahl Infektionen einer bestimmten Generation der Virusvermehrung berechnen können. So können wir zum Beispiel die in China empirisch ermittelte Reproduktionszahl zwischen 2,4 und 3,3 in unsere Formel einsetzen. Damit erhalten wir folgende Tabelle für R = 2,4:
|
0 |
1 |
|
1 |
3 |
|
2 |
9 |
|
3 |
23 |
|
4 |
56 |
|
5 |
136 |
|
6 |
327 |
|
7 |
786 |
|
8 |
1886 |
|
9 |
4528 |
|
10 |
10868 |
|
11 |
26085 |
|
12 |
62606 |
|
13 |
150254 |
|
14 |
360612 |
|
15 |
865469 |
|
16 |
2077126 |
|
17 |
4985104 |
|
18 |
11964251 |
|
19 |
28714204 |
|
20 |
68914092 |
Die Werte sind auf ganze Zahlen gerundet. Die Tabelle sagt uns, dass 20 Generationen ausreichen, um knapp die Bevölkerung der Bundesrepublik anzustecken.
Wie lange dauert das?
Nun ist die Frage, wie lange das Virus für eine Generation braucht. Hier kann man mit unterschiedlichen Werten arbeiten. Aus den Zahlen aus China geht hervor, dass der Abstand zwischen zwei Generationen etwa 6 Tagen entspricht.
Hier gibt es zwei Begriffe Generationszeit und Serienlänge. Wenn ein Bakeriologe eine Kultur anlegt, vermehren sich die Bakterien durch Zellteilung. Hier ist R = 2. Die Zeit, die es braucht, um eine neue Generation zu erzeugen ist also identisch mit der Verdoppelungszeit. (Hieran sieht man ganz gut die Denke von Virologen bzw. Bakteriologen... Es gibt hier nur "Neuinfektionen", da ja das alte Bakterium durch die neuen ersetzt wird. In dieser Welt ist die Zahlenreihe, die die Taz zitiert hat, völlig korrekt.)
Da bei einer Epidemie der Wert R erst bestimmt werden muss, brauchen wir ein anderes Verfahren, um die Generationszeit abzuschätzen. Denn nur, wenn wir diese kennen, können wir aus den Meldungen der Neuinfektionen R bestimmen. Das geht so:
Angenommen Hugo steckt Hans an. Wenn nun auch Hans Symptome entwickelt, geschieht das typischerweise 5-6 Tage nachdem Hugo die ersten Symptome hatte. Diese Zeitspanne nennt sich Serienlänge. Man kann für Epidemien vereinfacht sagen: Die Generationszeit entspricht der Serienlänge. Auf dieser Website wird mit der Serienlänge 5,2 gerechnet, sofern man den Wert nicht ändert. Aber wir wollen mit den optimistischeren 6 Tagen fortfahren. Update: Das Robert-Koch-Institut rechnet mit Zahlen zwischen 6 und 10. Dort werden die Zahlen aber auch als bewusst moderat bezeichnet.
Das bedeutet für unsere Tabelle für R = 2,4, dass nach 120 Tagen ungebremster Ausbreitung die gesamte Bevölkerung der Bundesrepublik infiziert ist.
Nehmen wir mal einen anderen Wert für R, nämlich den Mittelwert zwischen 2,4 und 3,3. Das ist 2,85. Dann erhalten wir folgenden Verlauf:
| 0 | 1 |
| 1 | 4 |
| 2 | 12 |
| 3 | 35 |
| 4 | 101 |
| 5 | 289 |
| 6 | 825 |
| 7 | 2352 |
| 8 | 6705 |
| 9 | 19110 |
| 10 | 54465 |
| 11 | 155226 |
| 12 | 442396 |
| 13 | 1260829 |
| 14 | 3593363 |
| 15 | 10241086 |
| 16 | 29187096 |
| 17 | 83183224 |
Hier braucht es schon nur noch 102 Tage, um eine „Durchseuchung“ zu erreichen.
Nun müssen wir noch etwas nachreichen, was den einen oder anderen Leser vielleicht schon beschäftigt hat. Wie berechnet man die täglichen Infektionswerte? Dies ergibt sich durch die Formel
It = R(t / T)
wobei T die Serienlänge und t die Anzahl an Tagen ist für die wir die Infektionszahl berechnen.
Das ist eigentlich ganz simpel, wenn man bedenkt, dass log(R) die Steigung einer Geraden auf der exponentiellen Skala ist. Teilt man die Steigung durch T, wird die Kurve genau so gestreckt, dass ein Wert für die Generation n erst nach n * T Tagen erscheint:
log(It) = log(R) * t / T
Wir sind nur 83 Millionen...
Die Kurve läuft aber nicht bis ins Unendliche so steil nach oben.
Zunächst einmal ist es so, dass wir nur eine begrenzte Anzahl an Personen haben, die wir anstecken können. Dafür können wir die Bevölkerung der Bundesrepublik mit ca. 83 Millionen Einwohnern ansetzen. Zur Zeit gibt es ohnehin keine großen Durchmischungen mit anderen Ländern mehr, also können wir sagen, dass das Wachstum spätestens dann aufhört, wenn die Bevölkerungszahl erreicht wird. Das Berechnungsmodell, dass dafür eingesetzt wird ist das so genannte SI-Modell.
Diesem liegt wiederum ein anderes Berechnungsmodell zugrunde, nämlich die Logistische Differenzialgleichung. Lassen Sie sich nicht von diesen Begriffen schrecken. Hier gibt es ein Video, das die zugrunde liegende Mathematik sehr anschaulich beschreibt.
Letztlich wird die Logistische Differenzialgleichung der Tatsache gerecht, dass wir eine begrenzte Ressource haben, die wir durch einen zunächst exponentiellen Verlauf ausschöpfen. Wir nähern uns rapide der Grenze und werden dann ausgebremst. Die Formel dafür ist etwa:
= N*1/(1+e (-k*N*t/T) *(N-1))
wobei N die Bevölkerungszahl, also 83 Mio ist, t und T unsere bekannten Werte der verstrichenen Tage und der Generationszeit. Nun ist da noch so eine Konstante k, die beim Lösen der Differenzialgeichung entsteht. Diese Konstante muss man für die jeweilige Anwendung der Gleichung bestimmen. In unserem Fall ist das
k = ln((N-1)/(N/R-1))/N
Ich lasse die Formel uneditiert, man kann sie so, wie sie ist, direkt in Excel einsetzen. Die Formel kann man möglicherweise vereinfachen, aber für unsere Zweckt tut sie es.
Update 12.04.2021: In der Praxis verwendet kein Mensch diese Formeln, weil man die simplen Differenzialgleichungen, aus denen diese komplizierte Formel hervorgeht, direkt in Computerprogrammen ausrechnen kann. Das habe ich in meinem Artikel über das SIR-Modell getan und daraus stammt auch das folgende Diagramm.
Update 22.04.2020: Als Nebenprodukt meines Artikels über das SIR-Modell ist das SI-Modell als Spezialfall herausgekommen, sodass ich dieses neue Diagramm hier zeigen möchte:
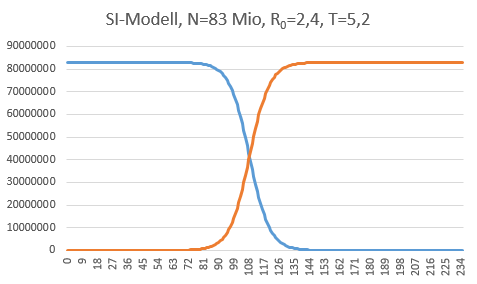
Die braune Kurve ist die Anzahl der Infektionen, die blaue Kurve die Anzahl der noch nicht Infizierten.
Man sieht, dass der Verlauf exponentiell bis in die Nähe der Gesamtbevölkerung steigt, bis er sich dann an die Zahl N anschmiegt. Aber ist der Verlauf am Anfang wirklich noch exponentiell? Und wie lange? Das kann man wiederum sehen, wenn man sich die Zahlen auf einer logarithmischen Skala ansieht. So lange der Verlauf exponentiell ist, müsste er auf der logarithmischen Skala eine Gerade ergeben:
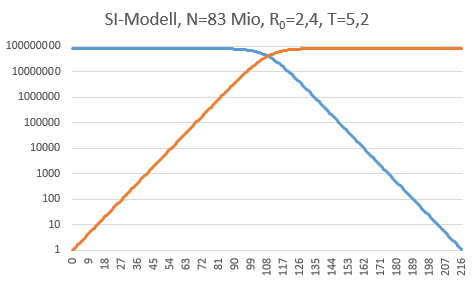
Nun sehen wir schon klarer: Es gibt einen ungebremsten Verlauf der Ausbreitung bis über die 10 Mio-Grenze hinweg, die wir nach knapp 100 Tagen erreichen.
Berücksichtigung der Immunisierung
Diese Formel ist aber auch noch nicht der Weisheit letzter Schluss. Wir haben nämlich noch nicht die Immunisierung berücksichtigt.
Dazu müssen wir uns klarmachen, dass R im Lauf der Zeit nicht konstant = R0 ist, sondern dass R kleiner wird, je mehr Menschen sich bereits infiziert haben. Jeder steckt durchschnittlich R0 Personen an, solange die Wahrscheinlichkeit, auf eine immune Person zu treffen, praktisch 0 ist. Bezogen auf unsere Generationen, können wir nun diese Wahrscheinlichkeit angeben als
W = In / N
wobei I die Gesamtanzahl der Infizierten in der Generation n ist und N die Bevölkerungsanzahl. Soviel sei gesagt: Es handelt sich um das SIR-Modell, also eine Erweiterung des SI-Modells unter Einbeziehung der Immunität. Man kann das SIR-Modell nicht mehr mit einer einzigen Formel darstellen. Aber es ist numerisch relativ leicht zu lösen. Den Weg dorthin zeigt dieses phantastische Video. Update 22.04.: Mittlerweile gibt es von mir eine Implementierung in C#, mit der Sie ein wenig herumprobieren können.
Aber ein Wissenschaftler namens Gabriel Goh hat sich bereits die Arbeit gemacht und einen Pandemie-Rechner zur Verfügung gestellt, bei dem man den Verlauf der Kurven mit der Veränderung der einzelnen Parameter betrachten kann:
http://gabgoh.github.io/COVID/index.html
Da kann man dann sehen, welche Größen in die Berechnung einfließen und man sieht auch ganz schön den Verlauf bis zum Maximum und den abschwingenden Ast danach, der durch die Immunisierung entsteht:
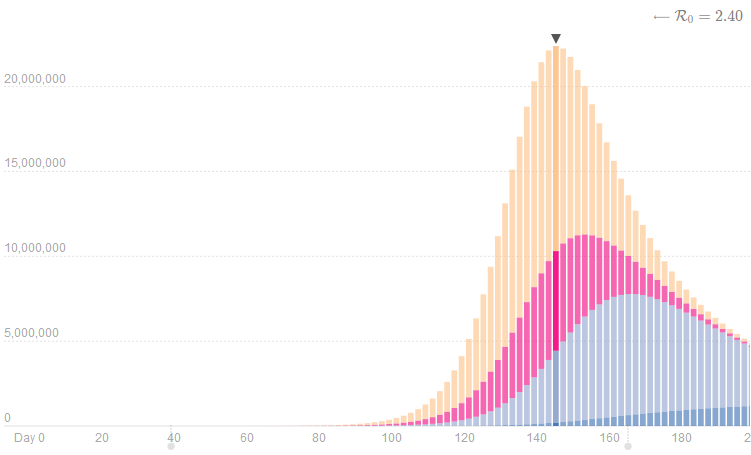
Diese Berechnung zeigt, dass nach gut 140 Tagen ein Maximum von etwas über 20 Mio Infektionen erreicht wird. Das entspricht über 7 Mio Fällen, die im Krankenhaus behandelt werden müssen (hellblaue Kurve).
Update: Erst jetzt hat mich jemand auf diese Publikation des Robert-Koch-Instituts aufmerksam gemacht. Hier sieht man, welche Parameter in die Berechnungen eingeflossen sind. Das kann man sehr gut abgleichen mit den Parametern des Pandemie-Rechners. In der Publikation wird mit R = 2 und einer Generationszeit von 10 Tagen gerechnet. Das ist eine sehr moderate Auslegung, wie der Autor selbst sagt (S. 10). Ende Update.
In dieser Stellungnahme der Deutschen Gesellschaft für Epidemiologie werden auf S. 3 ebenfalls Parameter der Modellrechnung genannt.
Eine Studie unter Nutzung der Ähnlichkeit der Kurve mit einer Gauss-Kurve findet sich hier. Der Autor versucht in seiner Modellrechnung das Ende der ersten Infektionswelle zu berechnen.
Update 20.05.: An dieser Stelle ging ich auf eine ominöse 27%-Linie in den Auswertungen von David Kriesel ein. Da David diese Linie vor einiger Zeit aus seinen Auswertungen entfernt hat, wurde der Absatz gestrichen. Ende Update.
Rein mathematisch gesehen ergibt sich folgende Erkenntnis aus dem bisher gesagten:
- Die Infektionszahlen zeigen einen exponentiellen Verlauf mit sehr hohen Werten bereits nach kurzer Zeit.
- Es gibt nur eine Größe, die wir beeinflussen können, um die Folgen der Corona-Pandemie einigermaßen im Rahmen zu halten, und das ist R.
- Kleine Änderungen im flachen Verlauf der Kurve haben nach wenigen Tagen sehr große Auswirkungen.
Ist das wirklich so einfach?
Nun ist die Frage berechtigt: Kann man ein so komplexes Geschehen wie eine Pandemie überhaupt mit ein paar mathematischen Formeln berechnen?
Ja, zumindest mit dem Corona-Virus*, mit dem wir es gegenwärtig zu tun haben. Nein, wenn wir damit die Verbreitung der Masern oder der Influenza berechnen wollten.
Warum ist das so? Weil einige Umstände, die die Berechnung komplexer machen würden, bei Corona schlichtweg wegfallen:
- Wir haben derzeit noch kaum Immunisierung, also eine ungebremste Rate R
- Die Regenerationsrate liegt ein gutes Stück über 1, wir haben ein beständiges Wachstum
- Die Verbreitung geschieht, bevor Symptome auftreten, bevor sich die Infizierten also krank ins Bett zurückziehen
Es gibt also nur ganz wenige Faktoren, die auf die Regenerationsrate R wirken: Das ist die durchschnittliche Häufigkeit physischer Begegnungen und die Immunisierung, die gegenwärtig in einem ganz geringen Bereich liegt.
Und weil das so einfach zu berechnen ist, kann man aufgrund der Zahlen aus China auch ganz gut abschätzen, wie hoch die Letalität (Todesrate im Vergleich zu den Fallzahlen) ist und wie stark die Gesundheitssysteme durch akute Infektionen belastet werden.
Da die Letalität vom Zustand des Gesundheitssystems abhängt, ist es eine der vordringlichen Aufgaben, eine Überlastung des Gesundheitssystems zu vermeiden. Die Anzahl an Fällen, die Intensivbetreuung benötigen, sollte möglichst weit unter der Anzahl der zur Verfügung stehenden Betten liegen. Ausführlichere Erwägungen dazu können Sie unter anderem hier nachlesen.
Die Folgerung aus diesem Artikel ist eindeutig, da gibt es keine Diskussion. Und die Regierungen weltweit lassen sich von solchen oder ähnlichen Berechnungen leiten, wenn sie eine Einschränkung der Bewegungsfreiheit der Bevölkerung anordnen.
Interessant war zu beobachten, wie Englands Premier Boris Johnson noch vor kurzem das Konzept der kontrollierten Immunisierung ("Durchseuchung") der Bevölkerung favorisiert hat und mittlerweile komplett umgeschwenkt ist auf die in anderen Ländern bereits eingeführten Einschränkungen der Bewegungsfreiheit. Ich schätze, da hat ihm jemand einmal den Zusammenhang zwischen Infektionszahlen und benötigten Intensivplätzen vorgerechnet.
Der exponentielle Charakter
Wir wissen nun, wie wir einen exponentiellen Verlauf von Messdaten erkennen können. Und dieser exponentielle Verlauf ist etwas, das Zahlenmengen auf eine fast klebrige Weise anhängt. Hat man einmal exponentielle Ausgangsdaten, so spiegelt sich der exponentielle Charakter in allen Daten, die wir daraus ableiten. Und das kann hilfreich sein, wenn man die Gefährdung aus den zur Verfügung stehenden Zahlen abschätzen will.
Zum Beispiel gibt es Personen, die sagen, dass die Hälfte aller positiven Tests falsche Positive seien, weil die bei uns verwendeten Tests auf andere Arten von Corona-Viren ansprächen. Der Chef-Virologe der Charité, Christian Drosten, hat sich bereits zu diesem Vorwurf geäußert und ihn entkräftet. Die RNA-Spuren, auf die der Test anspricht, stammen von Corona-Viren, die es heute nicht mehr gibt. Glücklicherweise sprechen die Tests aber auf SARS-CoV-2 an.
Ob das wirklich so ist, kann ich natürlich nicht beurteilen. Aber auf Basis unseres Wissens über Exponentialfunktionen können wir folgendes sagen: Wenn wir R durch zwei teilen — in der Annahme, nur die Hälfte der positiven Tests seien tatsächlich SARS-CoV-2-Positiv —, erhalten wir dennoch eine Exponentialfunktion. Das Problem bleibt damit das gleiche, man hat nur minimal mehr Zeit. Wir erreichen bei T = 5,2 und R = 2,4 die 83 Mio-Grenze nach ~78 Tagen, während wir bei R = 1,2 nach ~120 Tagen so weit sind.
Ein weiterer Aspekt sind die Todesfälle durch COVID-19. Dazu können wir folgendes sagen: Es gibt einen Zusammenhang zwischen den tatsächlichen Fällen, deren Zahl wir nicht kennen und den tatsächlich identifizierten Todesfällen. Wir wissen: durchschnittlich drei Wochen nach der Infektion wird ein gewisser Prozentsatz der tatsächlichen Fälle als Todesfälle auftauchen. Also wird der Verlauf der tatsächlichen Fälle denselben Charakter haben wie der Verlauf der Todesfälle. Ist letzterer exponentiell, werden auch die tatsächlichen Infektionen exponentiell verlaufen.
Nun gibt es Personen, die sagen, dass die Todesfälle eigentlich andere Fälle von akuten Atemwegserkrankungen sind, die „zufällig“ auch das an sich harmlose Corona-Virus* aufweisen. Schauen wir uns einmal den Verlauf der akuten Atemwegserkrankungen (ohne COVID-19) an (Quelle: Robert Koch Institut):
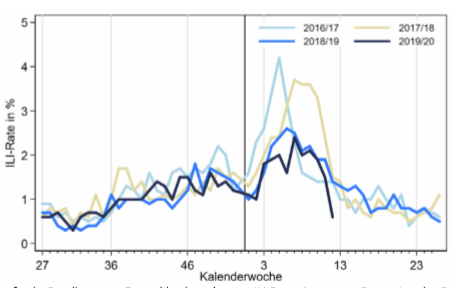
Die dunkle Linie ist der diesjährige Verlauf. Wir sehen in den letzten 5-6 Wochen eine stark fallende Tendenz der gemeldeten Fälle. Und nun schauen wir uns die Todesfälle mit Corona-Beteiligung an:
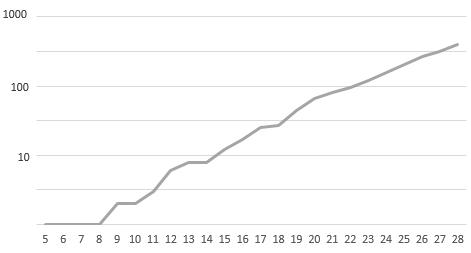
Wir haben die Daten auf einer logarithmischen Skala aufgetragen, weil wir ja wissen, dass ein exponentieller Verlauf auf einer logarithmischen Skala eine Gerade ergibt. Und eine bessere Gerade als in diesem Diagramm kann man sich gar nicht vorstellen. Im unteren Bereich zappelt die Kurve etwas, weil wir dort sehr wenige Fälle haben. Später wird der Verlauf glatter. Der Verlauf der Todesfälle entspricht überhaupt nicht dem Verlauf der Atemwegserkrankungen. Was wir suchen, ist eine Quelle mit einem exponentiellen Verlauf und das ist nicht die Rate der Atemwegserkrankungen.
Nun ist die Frage: Welcher Theorie ist man eher geneigt, zu glauben: Dass die Todesfälle mit den diversen akuten Atemwegserkrankungen zu tun haben, oder dass sie einem vermuteten exponentiellen Verlauf der tatsächlichen Fälle von COVID-19 folgen?
Zu guter Letzt wollen wir uns einem Artikel widmen, in dem eine hochinteressante Theorie geäußert wird. Dass nämlich der exponentielle Anstieg der bestätigten Infektionen damit zu tun hat, dass die Anzahl der Messungen exponentiell steigt, und damit ein Artefakt der Messungen ist. Daher wollte der Autor des Artikels, Paul Schreyer, vom Robert-Koch-Institut wissen, welche Anzahl an Messungen deren Fallzahlen zugrunde liegen.
Für die KW 11 und 12 erschienen dann tatsächlich die Zahlen. Und die interpretiert Herr Schreyer so, dass die Zahl der gemeldeten Infektionen verglichen mit der Anzahl der Messungen einen kaum merklichen Anstieg ergibt und daher auch die Zahl der tatsächlichen Infektionen kaum ansteigt. Der Autor teilt also die Zahl der Neuinfektionen durch die Anzahl Messungen und erhält dadurch eine Rate von 5,9 bzw. 6,8%. Besser gesagt, er musste es gar nicht selbst tun, denn das RKI hat das so veröffentlicht (S. 6):

Nun können wir ein schönes Verfahren der Mathematik anwenden. Wir nehmen die These von Herrn Schreyer als Voraussetzung an und sehen einmal, wohin uns das führt. Geraten wir durch die These in Widersprüche, können wir sie verwerfen.
Die These lautet in etwa: Egal, wieviel Tests wir vornehmen, wir kommen immer in etwa auf die gleiche Rate von etwa 6-7% positiver Fälle. Die gemeldete Anzahl an Infektionen ist also nahezu ausschließlich abhängig von der Anzahl der Tests. Und wenn diese exponentiell stiege, stiege auch die Anzahl an positiven Tests exponentiell.
Aus diesem Ansatz folgt, dass wir seit geraumer Zeit einen nahezu konstanten Stand an Infektionen hätten, der um die 6% liegt, mit einer leichten Steigerung in der KW 12 von 5,9 auf 6,8%, die wir hier vernachlässigen können. Wir rechnen mit 6% weiter.
Damit diese Rechnung aufgeht, müssen wir von durchschnittlich 6% Infektionen in der Bevölkerung ausgehen, das wären satte 4.980.000 Infektionen. Nehmen wir einmal an, die Letalität von COVID-19 läge wie bei der Grippe bei 0,2%. 0,2% sind ein Faktor von 0,002, das ergäbe 9.960 Todesfälle, bzw. 0,6%, mit denen Herr Schreyer rechnet, ergäben 29.880 Todesfälle. Die weltweit durchschnittlichen ca. 4% wären 199.200. Als dieser Artikel entstand, hatten wir in Deutschland 557 Todesfälle. (Update: In einer ersten Version des Artikels waren meine Faktoren um den Faktor 100 falsch. Sorry nochmals.)
Man merkt schon an der Größenordnung, dass hier irgendetwas nicht stimmen kann. Und das ist jetzt ein wichtiger Punkt: Eine These muss mit den vorhandenen Zahlen harmonieren. Man kann sie vielleicht durch eine abenteuerliche Theorie mit den tatsächlichen Zahlen in Einklang bringen, aber das ist halt wenig zielführend. Hier setze ich dann Ockhams Rasiermesser an.
Aber das eigentliche Argument ist wie folgt: Wir sehen einen exponentiellen Anstieg der Todesfälle mit Corona*-Infektion. Das kann Zufall sein, das kann aber auch einem exponentiellen Verlauf der tatsächlichen Infektionen folgen. Was ist wahrscheinlicher? Meine Erfahrung sagt, dass ein exponentieller Verlauf nie zufällig entsteht. Er stammt immer aus einer exponentiell wachsenden Quelle.
Und eins dürfen wir bei allen Betrachtungen nicht vergessen. Wir sind in Deutschland nicht allein auf der Welt. Italien zeigt einen massiven Anstieg an intensivmedizinischen Fällen, alle mit den gleichen Symptomen, alle Corona-positiv*. Was wir nicht sehen, ist ein entsprechender Anstieg anderer Atemwegserkrankungen in Italien. Was wir aber sehen, sind 10.000 Todesfälle in den letzten paar Wochen, die Corona-positiv sind. Was wir ebenfalls sehen, sind die exponentiellen Verläufe der gemeldeten Infektionen und der Corona-positiven Todesfälle weltweit.
Mein mathematisches Gefühl sagt mir also: Wir müssen auf der Hut sein, wir brauchen mehr Tests, um den tatsächlichen Stand der Infektionen überprüfen zu können. Und wir müssen alles tun, um den Wert R zu drücken.
Folgenden Satz finden wir in dem Artikel von Herrn Schreyer:
»Den aktuellen Daten des RKI (27.3.) zufolge beträgt der Anteil der Verstorbenen an den positiv Getesteten 0,6 %. Deren Durchschnittsalter (!) liegt laut Aussage von RKI-Chef Wieler bei 81 Jahren. Daraus lässt sich kaum eine extreme Gefährdung für die gesamte Bevölkerung ableiten.«
Das kann man behaupten, wenn man seine eigenen Zahlen nicht zu Ende rechnet. Von der Haltung gegenüber dem älteren Teil unserer Gesellschaft wollen wir erst gar nicht sprechen. Man könnte die Sache aber auch anders sehen:
Eine mögliche Interpretation der Zahlen
Wir stehen am Anfang eines exponentiellen Ausbreitungsverlaufs einer Krankheit, die nur entweder ganz leichte oder ganz schwere Fälle kennt. Die bisher aufgetretenen Fälle und der kurze Zeitraum, innerhalb dessen das Corona-Virus* sich ausbreitet, führte in Deutschland bislang nur zu wenigen Todesfällen von ohnehin vorbelasteten älteren Mitbürgern. Wenn sich aber die Krankheit erst einmal richtig in der Bevölkerung breit gemacht hat, nehmen auch die Todesfälle von jüngeren, gesünderen Personen zu. Die Wahrscheinlichkeit ist geringer, aber mit Zunahme der Infektionen wird auch aus einer geringen Wahrscheinlichkeit ein hoher Wert.
Ähnlich verhält es sich mit der Letalität (=Todesfälle / gemeldete Infektionen). Sie mag im Verlauf der Zeit leicht sinken, weil diejenigen dahingerafft sind, die dem Virus nicht so viel entgegenzusetzen haben. Dafür steigt aber die Zahl der Infizierten exponentiell und wird sehr bald die ganz großen Zahlenbereiche erreichen. Wenn man diese Zahlen mit einer geringeren Letalität multipliziert, kommt immer noch ein erschreckendes Ergebnis heraus.
Das ist unsere Interpretation der Zahlen, die für uns so lange gilt, bis jemand mit einer besseren Interpretation aufwarten kann.
Fazit
Mit Hilfe von wenigen Parametern lässt sich der theoretische Verlauf der Corona-Pandemie relativ leicht berechnen. Dazu haben wir den Einsatz der Exponentialfunktion beschrieben. Der wichtigste Parameter für den Verlauf der Krankheit ist die Regenerationsrate R. Diese lässt sich durch Maßnahmen senken, die geeignet sind, die Häufigkeit physischer Nähe zwischen Personen zu verringern. Warum das so ist und wie lange das beibehalten werden muss, ist in diesem Artikel recht gut erklärt. Wir hoffen, dass das Wissen über die Exponentialfunktion dazu beiträgt, bei den vielen Diskussionsbeiträgen den Weizen von der Spreu zu trennen.
* Jede Erwähnung des Corona-Virus in diesem Artikel meint den Typ SARS-CoV-2, wenn nicht explizit anders angegeben.