Corona: Die Berechnung von R

Update 24.05.: Mittlerweile gibt es vom RKI eine Beispiel-Tabelle zur Berechnung von R und dem geglätteten Wert R7. Leider befinden sich die angegebenen Formeln nicht mehr in den regelmäßig aktualisierten Tabellen, sondern nur die berechneten Werte.  In diesem Dokument wird die Berechnung erläutert. Ich werde am Ende des Artikels ein paar Aspekte der Vorgehensweise erläutern. Ende Update.

Als Reaktion auf meinen Artikel Ein wenig Corona-Mathematik fragte ein Leser, ob es eine Formel gäbe, mit der man den Wert R berechnen könnte, um die vom RKI veröffentlichten Werte nachvollziehen zu können. Ich habe dann basierend auf meinen bisherigen Erkenntnissen ein Verfahren aufgezeigt, mit dem sich eine Abschätzung von R berechnen lässt. Erst neulich bin ich über einen Text gestolpert, in dem erklärt wird, wie das RKI tatsächlich den Wert R berechnet. Zitat:

Bei einer konstanten Generationszeit von 4 Tagen ergibt sich R als Quotient der Anzahl von Neuerkrankungen in zwei aufeinander folgenden Zeitabschnitten von jeweils 4 Tagen.

Sprich: Wir addieren die Neuinfektionen aus einem Zeitraum von 4 Tagen auf, dann addieren wir die Neuinfektionen aus dem 4-Tage-Zeitraum davor auf und teilen die erste Summe (die neueren Werte) durch die zweite (die älteren Werte).

Die 4 Tage werden deshalb gewählt, weil man von einer durchschnittlichen Generationszeit von 4 Tagen ausgeht. Warum das so ist, wird im gleichen Kontext erklärt, das können Sie dort nachlesen (S. 13).

Ich habe die Werte der Infektionen über die Zeit in eine Excel-Tabelle eingetragen und mit Hilfe des vom RKI angegebenen Verfahrens die Werte von R über die Zeit berechnet. Der Verlauf sieht folgendermaßen aus:

 

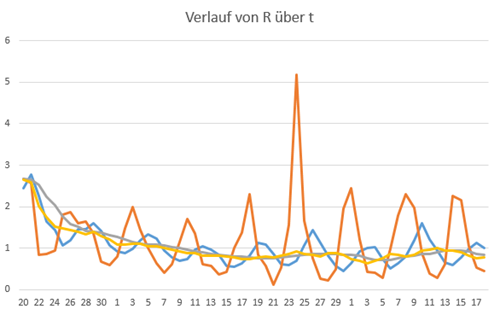
Die Berechnung nach Definition des RKI ist im Bild die blaue Kurve.

Die Kurve zeigt einen intensiven wellenförmigen Verlauf, der vom Meldeverhalten kommt*. Die Periode der Wellenbewegung beträgt 7 Tage. Als braune Kurve habe ich meine eigenen Berechnungen mit der Steigung der logarithmierten Werte ins Diagramm übernommen, wie ich sie in meinem Kommentar zum Thema "Formel" beschrieben habe. Der Verlauf zeigt noch größere Schwankungen, was nicht verwunderlich ist, weil die RKI-Werte bereits eine gewisse Glättung erfahren. Etwas genauer könnte man die Werte noch erhalten, wenn man über die Werte der letzten 4 Tage eine lineare Regression berechnet. Wir werden im Folgenden aber sehen, dass das gar nicht nötig ist.

Trotz der Unterschiede der blauen und braunen Kurve sieht man, dass sich die Werte im selben Bereich bewegen. Die Maxima des wellenförmigen Verlaufs sind um ein paar Tage zueinander verschoben, was aus der Glättung der Werte durch's RKI resultiert. Wahrscheinlich müsste man die Werte dem mittleren Datum des jeweils gemittelten Bereichs zuordnen, statt dem Ende, wie es bei der blauen Kurve der Fall ist. Das würde die Werte der blauen Kurve um zwei Tage nach links verschieben.

So kann ich nicht arbeiten!

Aber wie auch immer: Mit solchen Daten kann man sowieso nicht arbeiten. Eine Tendenz ist nur mit Schwierigkeiten erkennbar.

Daher bietet sich folgendes Verfahren an: Jedem Tag ordnet man einen Mittelwert der einzelnen Werte R aus den letzten 7 Tagen incl. des gegenwärtigen Tags zu. Damit erhält man eine Glättung der Kurve und die wöchentlichen Schwankungen verlieren sich. Die graue Kurve entspricht dem Berechnungsverfahren des RKI (soweit ich es verstehe), die gelbe Kurve ist mein Verfahren. Man sieht: die beiden Verfahren kommen auf's Gleiche heraus, die Kurven sind nahezu deckungsgleich. Das Verfahren des RKI funktioniert allerdings nur mit ganzzahligen Werten für die Generationszeit.

Man sieht bei beiden Verfahren einen Anstieg im Bereich 05.05.-13.05. der ziemlich hart am Wert 1 kratzt. Das bedeutet in der Praxis, dass die Anzahl der Neuinfektionen in diesem Zeitraum praktisch nicht abnimmt.

Was kann man nun an dem Wert R sehen? Er beschreibt die Dynamik des Verlaufs der Neuinfektionen, wobei Werte über 1 einer exponentiellen Steigerung entsprechen.

Der Wert kann nicht isoliert betrachtet werden, man muss immer den gegenwärtig aktuellen Stand der Neuinfektionen kennen. Dieser Stand entspricht dem Anfangszustand einer Prognose, die man vom gegenwärtigen Tag an rechnen kann.

Was ist jetzt mit der Verdopplungszeit?

Für Irritationen hat gesorgt, dass die Virologen (und damit auch die Regierung) für eine gewisse Zeit die Verdopplungszeiten veröffentlicht haben, um später in den Veröffentlichungen auf den Wert R zurückzukommen. Beides sagt dasselbe aus. Die Verdopplungszeit wird kürzer, je größer R ist und wird länger, je länger die Generationszeit T ist. Da T annähernd konstant ist, hängt die Verdopplungszeit im Wesentlichen von R ab.

Wenn wir einen Faktor f angeben wollen, um den die Anzahl der Neuinfektionen bei einem angegebenen Wert R täglich steigt, dann ist f:

f = e^ln(R)/T

Wir suchen die Zeit t, sodass

f ^t = 2

Daraus ergibt sich für die Verdopplungszeit t:

t = T * ln(2) / ln(R)

Und das ist jetzt ein wenig doof, weil ln(R) für R = 1 null werden kann. Null im Nenner ist immer schlecht. Die Formel beschreibt eine Hyperbel, die für R = 1 von positiven Werten her kommend positiv unendlich wird. Die Formel funktioniert daher nur für Werte R > 1 richtig.

Wie kommen die Leute nun darauf, für Werte von R < 1 eine Verdopplungszeit anzugeben? Ganz einfach: Man berechnet sie aus den aufakkumulierten Werten der Neuinfektionen, sprich: den Fallzahlen. In meinem ersten Artikel habe ich geschrieben, dass die Anzahl der Gesamtinfektionen annähernd einer Exponentialfunktion entspricht, die im Vergleich zum Verlauf der Neuinfektionen ein wenig nach oben verschoben ist. Daraus könnte man in etwa so etwas formulieren:

t = T * ln(2) / ln(R + v)

wobei v den Versatz darstellt. Das ist natürlich unbefriedigend. Daher: Berechnen Sie die Verdopplungszeit aus einem Wachstumsfaktor, den Sie aus dem Verlauf der Gesamtinfektionen der letzten 5 oder 7 Tage (je nach Publikation) ziehen können. Damit hat das Verfahren auch eine gewisse Ähnlichkeit mit dem Verfahren, mit dem das RKI den Wert R berechnet, und daran sieht man, dass beides dasselbe aussagt. Die Verdopplungszeit ist dann:

t = ln(2) / ln(q)

wobei q Ihr Wachstumsfaktor ist. Wenn ihnen das zu schwammig ist, geht es Ihnen wir mir und ich bleibe lieber bei R. Update 20.05.: Ich finde keine Quelle, wo das RKI mal zeigt, wie sie die Verdopplungszeit berechnen. Sie wird in einem Kontext erwähnt, in dem beschrieben wird, dass R = 1,3 einer Verdopplungszeit von 11 Tagen entspricht, aber das war's dann auch schon. Sie können ja jetzt einmal R = 1,3 in meine obige Formel einsetzen und nachrechnen.

Auswirkungen einer neuen Welle

Angenommen, wir können nicht verhindern, dass R wieder über 1 steigt und eine neue Welle beginnt. Die Maßnahmen sind aufgehoben und die Bevölkerung zeigt keine Bereitschaft, sich erneut einzuschränken. Dann bekommen wir wieder Werten von R um ~2. Der Trugschluss wäre nun, zu sagen: "Das hatten wir schon, also kriegen wir das wieder hin". Aber wir starten diesmal nicht mit einer Handvoll Infizierten wie im März, sondern mit ein paar Hundert Infizierten. Die Summe der gemeldeten Neuinfektionen der letzten 4 Tage beträgt 2.680, dazu kommt die Dunkelziffer, die wir jetzt mal vernächlässigen. Wenn wir ausgehend von diesem Sockel von 2.680 einen Infektionsverlauf mit R = 2 und T = 4 berechnen, dann sind wir innerhalb weniger Tage in hochgefährlichen Bereichen.

Eine Exponentialfunktion auf Basis dieser Parameter ergibt innerhalb von 21 Tagen (=durchschnittliche Erkrankungsdauer) zusammengenommen 570.000 Neuinfektionen. Setzen wir den Erfahrungswert von 5% Intensivfällen an, so sind wir bei ~28.000 belegten Intensivbetten. Ich gehe einmal davon aus, dass in dem Fall die Bereitschaft der Bevölkerung, erneut in Kontaktbeschränkungen zu gehen, rapide zunehmen wird, sodass diese Entwicklung sich nicht über 21 Tage fortsetzen wird. Hier sind wir wieder beim Thema The Hammer and the Dance.

Die Frage ist nun: Kann R überhaupt zurück in Wertebereiche um 2? Die Antwort darauf ist leider: ja. Denn wir haben von Südkorea eine sehr gute Analyse des Infektionsverlaufes durch ein exzellent organisiertes Tracking. Die hatten ja schon eine Pandemie hinter sich und wussten, wie sie das anfangen müssen. Die Analyse hat ergeben: Die berühmte Patientin Nr. 31 hat an zwei Tagen etliche Besucher einer Kirche angesteckt, sodass in wenigen Tagen darauf über 4.300 Infektionen daraus wurden.

Das Beispiel zeigt: COVID-19 ist eine hochansteckende Krankheit. Offensichtlich führen räumliche Nähe und Tätigkeiten wie Singen (Chorgesang), Gröhlen (Fußballstadium) etc., die belastete Aerosole aus dem Rachenraum in der Luft verteilen können, zu sehr hohen Verbreitungsraten. Durchschnittliche R-Werte von 2 und höher sind daher jederzeit möglich**.

Diese Gefahr bleibt bestehen, sofern nicht einer von vier Fällen eintritt:

1. Es gibt eine nennenwerte Immunisierung durch einen Impfstoff (den es möglicherweise nie geben wird).
2. Wir finden ein Medikament, mit dem der Erkrankungsverlauf im Schnitt weniger ernsthaft verläuft, sodass nicht so viele Intensivfälle daraus werden. Das wäre gut, weil dann eine "kontrollierte Immunisierung" denkbar wäre.
3. Wir halten R für eine Weile so tief, dass das Virus ausstirbt.
4. Wir können mit Tracking die mittlere Dauer der Infektiosität herabsenken, was ebenfalls R senken würde. Ich persönlich habe Zweifel daran, dass die an dem Projekt beteiligten Firmen eine App hinbekommen und dass das in der Praxis tatsächlich etwas bringt. Es erfordert ein hohes Maß an Beteiligung bei den Bürgern und ich kann die Bereitschaft dazu gegenwärtig nicht erkennen.

Update vom 24.05.:

Kommentar zur Erläuterung des RKI

Im Folgenden meine versprochenen R-läuterungen...

Die Erläuterung des RKI zur Berechnung von R beginnt im angegebenen Dokument auf S. 1 unten. Was hier zunächst unerwähnt bleibt, ist, dass die Berechnung nicht aufgrund der tatsächlichen Meldezahlen (nach Nowcast) erfolgt, sondern auf einer geglätteten Zahlenreihe. Hierzu wird der Durchschnitt der letzten vier Tage (incl. des Tages t) dem Tag t zugeordnet. Die ungeglätteten Zahlen befinden sich in der Spalte B der Beispiel-Tabelle, die mit "Punktschätzer der Anzahl Neuerkrankungen (ohne Glättung)" überschrieben ist. Für einen geglätteten Wert in der Zeile 5 lautet die Formel dann:

=SUMME(B2:B5)/4

Diese Formel ist im Dokument nicht angegeben, sondern nur die Werte, die dann mit "Punktschätzer der Anzahl Neuerkrankungen" überschrieben sind. Diese Glättung ist insofern bemerkenswert, als sie die wöchentlichen Schwankungen nicht ausgleichen kann. Die 4 Tage ermöglichen es aber, R mit einer einfachen Formel aus diesen geglätteten Werten zu berechnen.

Die Erläuterung beginnt dann mit einer Überlegung zu Wahrscheinlichkeiten, nämlich dass die Wahrscheinlichkeit, dass sich eine Neuerkrankung an einem der erkrankten Fälle aus den vergangenen Tagen angesteckt hat, in der Summe bei 100% liegt und auf jeden Tag aus der Reihe 1,2 ... t ein Teil dieser 100% entfällt (t ist der gegenwärtige Tag). Auf diese Weise entsteht eine Wahrscheinlichkeitsverteilung über die vergangenen Tage.

Es ist anzunehmen, dass die Wahrscheinlichkeitsverteilung ihr Maximum bei bei t - s hat, wobei s die Serienlänge ist, also der Zeitraum, der zwischen zwei Ansteckungsgenerationen durchschnittlich verstreicht (lt. RKI ist s = 4 Tage).

Diese Überlegungen zur Wahrscheinlichkeit sind für Statistiker möglicherweise von Belang, für die Berechnung spielen sie allerdings überhaupt keine Rolle. Für die Berechnung können wir sagen, dass sich die aktuellen Erkrankungen E_t typischerweise 4 Tage vorher angesteckt haben. Diese vereinfachte Formel wird dann auch im Artikel genannt:

R_t = E_t / E_t-4

Im Excel-Dokument der Beispielberechnungen ist dieses Verfahren in der Spalte "Berechnung 1 des R-Wertes" zu finden.

Im unteren Teil von S. 2 wird das gegenwärtig ausschlaggebende Verfahren zur Berechnung des 4-Tages-R beschrieben. Zunächst wird aus einer angegebenen Literaturquelle*** eine Formel übernommen, dann folgt die richtige Bemerkung, dass die dort genannte Formel einem gleitenden Mittelwert über die letzten 4 Tage entspricht. Damit kommen wir zu der Definition, die ich am Anfang dieses Artikels aus einem anderen Dokument des RKI zitiert habe. Für den Wert R in der Zeile 12 mit den ungeglätteten Ausgangswerten in der Spalte A ergibt sich folgende Formel:

=SUMME(A9:A12)/SUMME(A5:A8)

Im Beispiel-Excel-Dokument des RKI ist diese Spalte mit "Berechnung 2 des R-Wertes" überschrieben. Nun wird es Zeit, diese Zahlen in einem Diagramm zu veranschaulichen:

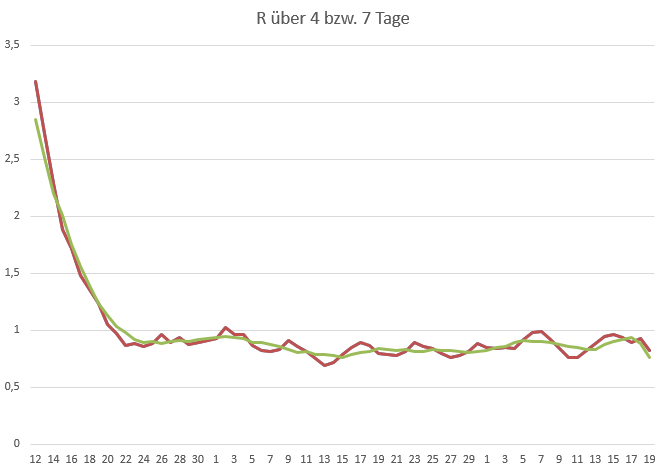
Das Diagramm enthält 3 (!) Kurven. Die braune Kurve ist die oben genannte Formel des gleitenden Mittelwerts über die ungeglätteten Werte der Neuinfektionen. Sie überdeckt die Werte einer blauen Kurve, die aus der zuerst genannten Formel 

R_t = E_t / E_t-4

über die geglätteten Ausgangswerte resultieren. Beide Berechnungsverfahren kommen auf die gleichen Resultate. Es spielt also keine Rolle, ob man zuerst glättet und dann den Quotienten E_t / E_t-4 bildet, oder ob man den gleitenden Mittelwert über die ungeglätteten Werte bildet.

R größer als 1?

Man sieht, dass keine dieser Kurven den Wert 1 im Mai übersteigt. Wie es also zu veröffentlichten Werten R > 1 im Mai kommen konnte, erschließt sich aus den aktuellen Zahlen nicht. Das liegt daran, dass die älteren Zahlen von den aktuelleren Zahlen aus dem neueren Nowcast überschrieben werden. Eine solche Überschreibung ist, gelinde gesagt, suboptimal. Aber der Darstellung der Tendenz tut es zunächst einmal keinen Abbruch.

Wenn aber die offizellen Zahlen für R von Anfang Mai nachvollzogen werden sollen, müssen dazu die Zahlen von Anfang Mai verwendet werden. Die muss man dann aus anderen Quellen als dem RKI nehmen.

Nun schwanken die Werte der braunen Kurve aber immer noch sehr. Für die Darstellung einer Tendenz ist der Glättungszeitraum immer noch zu kurz. Ideal wäre eine Woche, um die wochenabhängigen Schwankungen herauszuglätten. Das führt zu dem 7-Tage-R, das seit neuestem verwendet wird.

Die vom RKI dafür angegebene Formel in Excel ist für die Zeile 11:

=SUMME(A6:A12)/SUMME(A2:A8)

wobei sich in der Spalte A die ungeglätteten Werte befinden. Man nimmt also zwei Zeiträume, die 7 Tage lang sind, und um 4 Tage zueinander verschoben sind. Die gemeldeten Neuinfektionen dieser beiden Zeiträume werden wie beim 4-Tages-R aufaddiert und ein Quotient der neueren Werte im Zähler und der älteren Werte im Nenner gebildet. Das Resultat ist dann ein geglätteter Wert für R.

Aufmerksamen Beobachtern ist eventuell aufgefallen sein, dass Werte bis zur Zelle A12 herangezogen werden, um sie dem Tag in der Zeile 11 zuzuordnen. Dieser Versatz um 1 Tag wird im Text erklärt und diese Vorgehensweise ist absolut in Ordnung.

Für Leser, die schon einmal etwas von digitaler Signalverarbeitung gehört haben, entspricht die Vorgehensweise einem Filter, das Schwankungen mit einer gewissen Frequenz (1 / 7 Tage) herausfiltern kann. Solch ein Filter hat eine Signalverzögerung zur Folge, die dann durch die Verschiebung um einen Tag ausgeglichen wird. In der Signalbearbeitung hat man also das gleiche Problem und löst es auf die gleiche Weise.

Was ist der Nowcast?

Das RKI beschreibt in diesem Dokument, warum man nicht mit den direkten Meldedaten arbeiten kann, sondern die Daten in einer bestimmten Weise aufbereiten muss. Idealerweise möchte man alle gemeldeten Fälle ihrem Infektionsdatum zuordnen. Das ist aber nicht möglich, weil sich infizierte Personen erst melden, nachdem sie Symptome entwickelt haben. Der Zeitpunkt, der dem Infektionszeitpunkt am nächsten kommt, wäre das Datum, ab dem die ersten Symptome auftraten.

Aber auch dieses Datum ist bei vielen gemeldeten Fällen unbekannt. Zum Zeitpunkt der Veröffentlichung des Nowcasting-Verfahrens durch das RKI war der Erkrankungsbeginn nur in 62,5% aller Fälle bekannt. Diese geringe Quote erklärt sich zum Großteil dadurch, dass viele Erkrankungen ohne Symptome verlaufen.

Man betrachtet nun die Fälle, bei denen das Erkrankungsdatum bekannt ist und schlüsselt die Informationen auf. Man kann zum Beispiel sagen, dass bei Meldungen in einem bestimmten Zeitraum die Differenz des Meldedatums und des Krankheitsbeginns einem bestimmten durchschnittlichen Wert entspricht (aufgrund von Meldungsrückstau etc.).

Solche Informationen können nun auf die Fälle mit unbekanntem Erkrankungsbeginn zurückgerechnet werden, sodass sich daraus ein realistischeres Bild des Infektionsverlaufs ergibt. Eine solche Abschätzung fehlender Werte aufgrund von vollständigen Datensätzen nennt sich Imputation.

Im Endeffekt führt der Nowcast zu einer Verschiebung der Kurve der Neuinfektionen um eine gewisse Anzahl an Tagen nach links. Daraus ergibt sich, dass die Zahlen für die jüngsten paar Tage ungenauer sind, als die für die Vergangenheit, weil ein Teil der fehlenden Daten nachträglich eintrifft. Das kann man in dem Diagramm im angegebenen Dokument auf S. 14 ganz gut sehen.

Fazit

R ist ein Wert, der die Dynamik der Entwicklung von Neuinfektionen einer Epidemie beschreiben kann. Der Wert wird aus den zur Verfügung stehenden Daten zu den Neuinfektionen ermittelt und kann direkt als Parameter in Exponentialfunktionen bzw. komplexeren Modellen verwendet werden, die eine Prognose der weiteren Entwicklung einer Epidemie erlauben. Die gegenwärtige Entwicklung von R, zusammen mit dem gegenwärtigen Stand an Neuinfektionen zeigt, dass wir noch große Vorsicht walten lassen müssen.

______

* Das ist übrigens einer meiner großen Kritikpunkte am Meldewesen in Deutschland: Statt über eine zentrale IT-Lösung die Meldungen direkt in ein zentrales Register zu schreiben, werden Meldungen zum Teil per Fax verschickt. Es dauert im Schnitt mehrere Tage, bis die Meldungen beim RKI zusammenkommen. Wenn es jetzt Infektionswege gäbe, die sich auf reale Ereignisse im Wochentakt beziehen (z.B. Kirchgang), ließe sich dieser Sachverhalt aufgrund der Meldungszahlen nicht erkennen. Ein weiterer Schwachpunkt der Datenverarbeitung durch das RKI ist, dass der Datenbestand mit neuen Erkenntnissen überschrieben wird, sodass die Änderungen der Datensätze nicht nachvollziehbar sind, wenn man nicht selbst die Originaldaten aufhebt. Daher kommt die Forderung von Datenjournalisten ans RKI, besser aufbereitete Daten zur Verfügung zu stellen. Ein Schritt in die richtige Richtung ist die Initiative einer Firma, die in Kooperation mit dem RKI ein Corona-Dashboard auf Basis der aktuellen Daten zur Verfügung stellt. Das Dashboard ist schon mal ganz interessant, aber noch interessanter ist, dass es auf einer Json-basierten REST-Schnittstelle aufbaut, die jeder für seine eigenen Analysen nutzen kann. Wenn Sie das tun, cachen Sie die Daten, damit nicht jeder Zugriff auf Ihre Datenanalysen auf die Schnittstelle von argcis.com durchschlägt.

** Es ist noch nicht durch Studien belegt, aber es sieht so aus, als ob bestimmte Arten von Versammlungen zu einer großen Verbreitung führen, während der normale Kontakt zwischen Menschen, vor allem unter Einhaltung des Sicherheitsabstands, recht niedrige Verbreitungsraten zur Folge hat. Das würde auch erklären, warum die Werte für R, die aus China kamen, regional so unterschiedlich ausfielen. Das hängt davon ab, ob sich in einer Region ein ein oder mehrere Infektionscluster gebildet haben. Diese Ungleichverteilung lässt sich direkt aus dem Mechanismus der Verbreitung erklären. Es sieht also so aus, als ob die Reduzierung der gegenwärtigen Maßnahmen auf Sicherheitsabstand und Masken, die die Aerosolbildung hemmen, ausreicht, um R dauerhaft so tief zu halten, dass das SARS-CoV-2-Virus ausstirbt. Das werden wir wohl so ab Anfang/Mitte Juni genauer wissen. Update 17.07.: Das Aussterben können wir jetzt getrost als illusorisch bezeichnen.

*** Cori A, Ferguson NM, Fraser C, and Cauchemez S, "A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics", American Journal of Epidemiology, Volume 178, Issue 9, 2013, S. 1505–1512