Corona: Das SIR-Modell in C#
Dienstag, 21.04.2020
Gesundheitsexperten des Robert-Koch-Instituts haben mit Modellberechnungen politische Entscheidungen beeinflusst, die zu den gravierendsten des Jahrhunderts gehören könnten. Interessant daran ist, dass man die Modelle in C# relativ leicht nachvollziehen kann.
Das SIR-Modell
SIR steht für Suspectable, Infected, Removed. Es ist ein Modell, das von einer Gesamtbevölkerungszahl N ausgeht, in der sich eine Epidemie verbreitet. Die Suspectable-Gruppe sind die Personen, die noch angesteckt werden können, die Infected sind diejenigen, die schon infiziert wurden und die Removed sind diejenigen, die aus dem System genommen werden, entweder, weil sie wieder gesund sind oder weil sie bereits gestorben sind.
Dem System liegen drei Differenzialgleichungen zugrunde. Eine Differenzialgleichung beschreibt Änderungen einer Größe über eine Ausgangsgröße, in unserem Fall die Änderungen der Infektionen, der Suspectable und der Removed über die Zeit. Die entsprechenden Formeln sind auf Wikipedia beschrieben. Ich habe mich aber entschieden, aus Gründen der Einfachheit auf eine winzige Variation der drei Gleichungen zu bauen, die von Prof. Dr. Edmund Weitz auf phantastische Art und Weise auf Youtube beschrieben worden sind. In gut einer halben Stunde erklärt Dr. Weitz alles, was man wissen muss, um das SIR-Modell zu verstehen – und das auf eine ziemlich einfache und einleuchtende Art und Weise. Nebenbei erklärt er, warum man überhaupt Modellrechnungen vornimmt und was diese im praktischen Einsatz taugen.
Nun aber zum Modell. Die drei Gleichungen, um die es dabei geht, sind:
S' = dS/dt = -αSI
I' = dI/dt = αSI – βI
R' = dR/dt = βI
Sehen wir uns einmal die mittlere Gleichung für dI/dt an. Die Änderung der Anzahl an Infektionen über die Zeit ist proportional zur Anzahl der bestehenden Infektionen I, aber ebenso zur Anzahl der Personen, die noch infiziert werden können, also S. Bitte schaut Euch das Video von Dr. Weitz an, der erklärt das ganz wunderbar. Ich greife nur einen kleinen Aspekt der Erklärung heraus. αSI beschreibt die Zunahme der Anzahl, βI beschreibt einen dämpfenden Faktor der Zunahme, der dadurch entsteht, dass ein bestimmter Teil der Infektionen wieder aus der Berechnung wegen Genesung oder Tod herausfällt. Da wir am Anfang einer Epidemie weder Todesfälle noch Genesungen haben, ist βI = 0 und S ist eine Konstante, nämlich die Bevölkerungsanzahl. Denken wir uns kurz αS als eine Konstante γ, dann haben wir die Gleichung:
I' = γI
Wer nun noch eine dunkle Erinnerung an seine Mathestunden hat, dem wird auffallen, dass es nur eine Gattung an Funktionen gibt, deren Ableitung proportional zu den Ausgangswerten ist, und das sind Exponentialfunktionen.
Die Lösung der vereinfachten Differenzialgleichung I' = γI lautet:
It = c * eγt
Die Bestimmung der Parameter
In die Konstante γ = αS geht die Regenerationsrate R0 ein. Was wir für die spätere Berechnung suchen, ist der Faktor α in Abhängigkeit von R0.
In meinem ersten Artikel habe ich ja bereits beschrieben, dass wir die Neuinfektionen mit
Ineu = R0t
beschreiben können. Das kann man zur Basis e umformen:
Ineu = eln(R0)t
Gleichzeitig beschreibt Dr. Weitz in seinem Video die Konstante γ als
γ = αS(0) bzw. γ = αN, wobei N die Gesamtbevölkerungszahl ist, die am Anfang ja die Anzahl der gefährdeten Personen S darstellt.
Die Erkenntnisse können wir kombinieren und sagen:
αN = ln(R0)
und damit
α = ln(R0) / N
wobei R0 die Regenerationsrate (bei SARS-CoV-2 etwa 2,4 – 3,3) und N die Bevölkerungsanzahl ist.
Dr. Weitz macht es anders herum und leitet R0 aus vorhandenen Zahlen ab (die allerdings rein fiktiv sind). Dieses Kurvenfitting ist ziemlich simpel, wenn man alle Werte logarithmiert und dann eine Gerade durchfittet. Auf diesen Zusammenhang habe ich bereits in meinem ersten Artikel hingewiesen. Das brauchen wir hier aber nicht tun, da wir aus wissenschaftlichen Veröffentlichungen die Schätzungen von R0 kennen.
Aber es gibt noch einen anderen Grund, warum wir mit den veröffentlichten Messwerten nicht viel anfangen können: Wir wissen nichts über das Verhältnis der gemessenen Infektionen zur Dunkelziffer. Die wissenschaftlichen Schätzungen von R0 berücksichtigen die Dunkelziffer. Genau dafür brauchen wir ja Modellberechnungen. Wir wollen wissen, wie die Epidemie unter vorausgesetzten Werten von R0 bzw. R verläuft.
Zurück zu unseren Parametern. Nun brauchen wir noch einen Wert für β und das ist ziemlich simpel:
β = 1 / Tr
wobei Tr die Zeit ist, die eine typische Erkrankung dauert (r steht für removal). Der Wert bestimmt, nach wievielen Tagen eine Infektion wieder aus dem System fällt.
Nun müssen wir noch eine Kleinigkeit korrigieren. Beim gegenwärtigen Stand von α wären auf der X-Achse die Generationen zu sehen und nicht die Tage. Wir müssen die Darstellung um den Faktor T dehnen. Das heißt:
α = ln(R0) / N / T
Es gibt übrigens eine ganze Liste an Voraussetzungen, von denen dieses Modell ausgeht. Dazu sei wiederum auf das Video von Herrn Dr. Weitz verwiesen, der das sehr schön auseinandersetzt.
Tot oder gesund?
Will man das Modell ein wenig differenzieren, wird daraus das SIRD-Modell, das zwischen Gesundeten (Recovered) und Toten (Dead) unterscheidet. Die lassen sich aus dem gemeinsamen Faktor β berechnen, der besagt: Nach Tr Tagen fällt eine infizierte Person aus dem System, oder anders herum: Jeden Tag fallen 1/Tr der bislang Infizierten aus dem System. Dazu führen wir einen Letalitätsfaktor λ < 1 ein, das ist der Prozentsatz aller Infizierten, der stirbt. Die Gesundeten sind dann der Rest, also 1 - λ. Nun kann man die gesundeten mit Hilfe des Faktors β * (1 - λ) und die Todesfälle mit dem Faktor β * λ berechnen.
Die Formel für S' ist ebenfalls ziemlich einfach zu erklären: S nimmt mit der gleichen Rate ab, in der I zunimmt, nämlich mit -αSI.
Wie löst man jetzt diese Differenzialgleichungen? Das Ganze ist ja ein Gleichungssystem mit gegenseitigen Abhängigkeiten. Die Antwort ist: Man muss die Gleichungen gar nicht lösen. Mit Hilfe eines Programms können wir die Werte der einzelnen Gleichungen numerisch mit beliebiger Genauigkeit ermitteln. Das Programm geht von einem bestimmten Startwert aus (in unserem Fall: 1 infizierte Person zum Zeitpunkt 0) und berechnet mit Hilfe der Differenzialgleichungen jeweils den nächsten Wert für einen Wert t, der nur um eine Winzigkeit gegenüber dem letztem Wert t differiert. Man kann die Gleichungen also folgendermaßen in C# schreiben:
var dS = delta_t * ( -alpha * S * I );
var dI = delta_t * (alpha * S * I - beta * I);
var dD = delta_t * lambda * beta * I;
var dR = delta_t * (1-lambda) * beta * I;
dS wird numerisch zu einem kleinen ΔS, entsprechend dI, dD und dR. delta_t ist das winzig kleine Zeitintervall, um das wir in unserer Berechnung fortschreiten. Die Formeln sind also nichts anderes, als eine Umstellung der oben gezeigten Differenzialgleichungen.
Das Programm ist in C# wie folgt:
using System;
using System.IO;
namespace SIR_Modell
{
class Program
{
static void Main( string[] args )
{
new Program().DoIt();
}
const double N = 83000000; // Bevölkerungszahl
const double R0 = 2.4; // Regenerationsrate
const double T = 5.2; // Regenerationszeit
double beta = 1.0 / 21.0; // kombinierte Gesundungs- / Todesrate
double alpha; // ln(R0)/N
void DoIt()
{
alpha = Math.Log( R0 ) / N / T;
double Laufzeit = 300;
double Unterteilung = 100;
double lambda = 0.4 / 100; // 0,4%
CellArray ca = new CellArray();
// Startwerte
double I = 1;
double S = N - I;
double R = 0;
double D = 0;
ca[0, 0] = "Tag";
ca[0, 1] = "S";
ca[0, 2] = "I";
ca[0, 3] = "D";
ca[0, 4] = "R";
ca[1, 0] = 0;
ca[1, 1] = S;
ca[1, 2] = I;
ca[1, 3] = D;
ca[1, 4] = R;
var delta_t = 1 / Unterteilung;
for (int i = 0; i < Laufzeit; i++)
{
for (int j = 0; j < Unterteilung; j++)
{
var dS = delta_t * ( -alpha * S * I );
var dI = delta_t * (alpha * S * I - beta * I);
var dD = delta_t * lambda * beta * I;
var dR = delta_t * (1-lambda) * beta * I;
S += dS;
I += dI;
R += dR;
D += dD;
}
var row = i + 2;
ca[row, 0] = i + 1;
ca[row, 1] = S;
ca[row, 2] = I;
ca[row, 3] = D;
ca[row, 4] = R;
}
File.Delete( "result.csv" );
using (FileStream fs = File.OpenWrite( "result.csv" ))
using (StreamWriter sw = new StreamWriter( fs ))
ca.ToStreamWriter( sw );
}
}
}
Wir legen am Anfang die Parameter des Modells fest: R0, N, T, alpha, beta, sowie die Letalität lambda. Dazu kommen noch ein paar technische Parameter, nämlich die Anzahl an Tagen, wie lange die Simulation laufen soll und ein Wert, der angibt, wie fein wir die einzelnen Schritte unterteilen wollen. Hier habe ich den relativ willkürlichen Wert 100 gewählt. Für die Anzahl an Tagen habe ich das Programm einmal durchlaufen lassen, um zu sehen, in welchem Wertebereich die Musik spielt. Daraufhin habe ich die Anzahl an Tagen auf 300 festgelegt.
Das Programm durchläuft zwei Schleifen. Die äußere Schleife repräsentiert die einzelnen Tage. In dieser Auflösung wollen wir am Ende die Werte haben. Die innere Schleife teilt einfach die Tage noch einmal in 100 Einzelschritte auf. Jeweils nach 100 Einzelschritten halten wir den Zwischenstand fest.
Das Ergebnis wird mit Hilfe einer Klasse CellArray in eine Datenstruktur geschrieben, die wir bei der FORMFAKTEN GmbH verwenden, um CSV-Dateien für Excel-Auswertungen zu erzeugen.
Dieses CellArray wird am Ende in eine Datei geschrieben.
Das ist das Ergebnis:
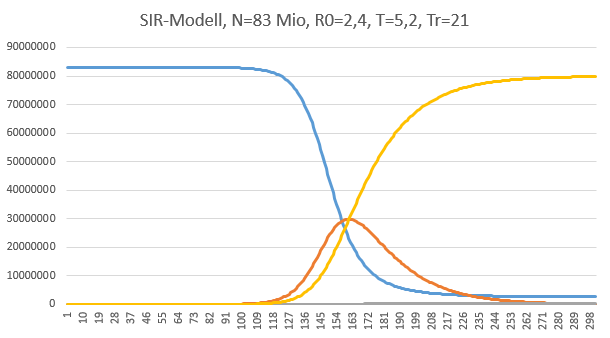
Die braune Kurve ist der Verlauf der aktiven Infektionen. Die blaue Kurve sind die Personen, die ansteckbar sind. Die gelbe Kurve sind die Genesenen. Und dann gibt es noch die graue Kurve am unteren Rand, das sind die Todesfälle.
Der Verlauf der Infektionen ist wie erwartet glockenförmig und deckt sich im Wesentlichen mit den Veröffentlichungen zu dem Thema. Man sieht, dass sich am Anfang, so in den ersten 100 Tagen, nichts tut, was der trügerische Effekt von exponentiellen Verläufen ist. Dann geht es relativ rapide. Innerhalb von gut 50 Tagen erreichen wir einen Stand von etwa 30 Mio Infizierten. Es gibt nun Schätzungen über den Prozentsatz an infizierten Personen, die ins Krankenhaus müssen, und denen, die eine Intensivbehandlung benötigen. Letztere werden auf etwa 5% der Infizierten geschätzt, sodass ein Bedarf von etwa 1,5 Millionen Intensivbetten entstehen würde. Ein solcher Schub an Infektionen würde das Gesundheitswesen um Größenordnungen überlasten.
Ich möchte noch einmal darauf hinweisen, dass die Anzahl der Infektionen fast ungebremst bis kurz vor Erreichen des Maximums exponentiell verläuft.
Das kann man sehr schön auf einer logarithmischen Skala sehen:
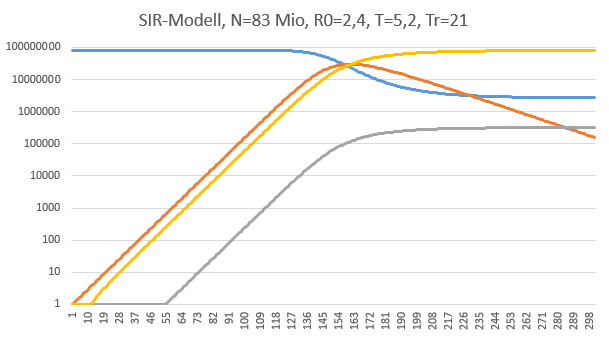
Um das Diagramm lesbarer zu machen, haben wir alle Resultatwerte < 1 auf 1 aufgerundet. Solange die Werte auf einer Geraden mit einer positiven Steigung verlaufen, haben wir einen exponentiell steigenden Verlauf.
Die graue Kurve zeigt die Todesfälle. Sie knickt erst nach Überschreiten der 100.000 nach rechts.
Das Argument gegen die "kontrollierte" Durchseuchung ist der exponentielle Verlauf der Infektionen bis fast zum Maximum. Hier kann man noch so hin- und herrechnen, es ergibt sich keine kontrollierbare Situation. Die Anzahl der Todesfälle wäre auch bei noch so gering angenommener Letalitätsrate eine Katastrophe.
Wir sollten uns bei diesen Modellberechnungen jederzeit darüber im Klaren sein, dass es sich hier nicht um exakte Berechnungen handelt, sondern um die Darstellung von Größenordnungen. Mehr kann und will ein Modell nicht leisten.
Ungleiche Verteilung als Vorteil
Eins ist vielleicht noch anzumerken: Das Modell geht von einer gleichmäßigen Verteilung der Infektionen aus. Das war bislang in Wirklichkeit nicht der Fall. Wir hatten ein paar Super-Spreading-Ereignisse (Ischgl, Heinsberg, etc.), wo die Regenerationsrate wesentlich höher anzusetzen war, und wir hatten Regionen, in denen sie wesentlich niedriger lag. Diese ungleiche Verteilung führte zwar dazu, dass die absoluten Infektionszahlen schneller in bemerkbare Regionen kamen, führte gleichzeitig aber im Weiteren zu einer besseren Beherrschbarkeit der Situation.
Gegenwärtig wird die Lockerung der Maßnahmen gegen die Ausbreitung des Virus diskutiert. Eine unbedachte Lockerung würde zu einer neuen Situation mit einer wesentlich breiteren Streuung der Infektionen führen, was eher unserem Modell entspricht und was weitere Infektionswellen eher unbeherrschbar macht. Daher warnen die Virologen zurecht davor.
Sie können das Programm verwenden, um selbst verschiedene Variationen der Verläufe durchzurechnen. Theoretisch ließe sich auch ein Verlauf berechnen, der sich ergäbe, wenn man ab sofort alle Maßnahmen zur Eindämmung der Epidemie aufheben würde. Das lässt sich mit entsprechenden Startwerten für S und I bewerkstelligen. Die Ergebnisse dürften klar machen, warum weiterhin Maßnahmen zur Eindämmung des praktisch erzielten Werts R nötig sind.
Man könnte auch den Wert R über die Zeit variieren und damit die Stärke und Lockerung der Maßnahmen simulieren. Damit lassen sich Verläufe mit einer zweiten Infektionswelle simulieren.
DISCLAIMER
Die angegebenen Verfahren und Formeln dienen der Veranschaulichung der Materie und können inkorrekt sein. Bitte verwendet für Fachdiskussionen geprüfte Verfahren. Ihr könnt mir gerne Hinweise auf Fehler schicken.
Im Anhang noch die Klasse CellArray.
public class CellArray : List<List<object>>
{
public CellArray()
: base()
{
}
int maxCol;
public object this[int row, int col]
{
get
{
if (row >= this.Count)
throw new Exception( "CellArray: Row mit Index " + row + " nicht vorhanden." );
List<object> rowList = this[row];
if (col >= rowList.Count)
return "";
object o = rowList[col];
if (o == null)
return "";
string s = o as string;
if (o is DateTime)
return ( (DateTime) o ).ToString( "yyyy-MM-dd hh:mm:ss" );
return o.ToString();
}
set
{
string valstr = value as string;
if (valstr != null)
{
if (valstr.IndexOf( ';' ) > -1 && valstr[0] != '"')
{
valstr = "\"" + valstr + "\"";
}
valstr = valstr.Replace( '\n', ' ' ).Replace( '\r', ' ' );
value = valstr;
}
while (Count <= row)
this.Add( new List<object>() );
List<object> rowList = this[row];
while (rowList.Count <= col)
rowList.Add( string.Empty );
rowList[col] = value;
this.maxCol = Math.Max( col + 1, maxCol );
}
}
public MemoryStream ToStream()
{
MemoryStream ms = new MemoryStream();
ToStream( ms );
ms.Seek( 0L, SeekOrigin.Begin );
return ms;
}
public void ToStream( Stream stream )
{
StreamWriter sw = new StreamWriter( stream, Encoding.UTF8 );
ToStreamWriter( sw );
sw.Flush();
}
public void ToStreamWriter( StreamWriter sw )
{
for (int r = 0; r < this.RowCount; r++)
{
int end = ColCount - 1;
for (int c = 0; c < ColCount; c++)
{
sw.Write( this[r, c].ToString() + ( c < end ? ";" : string.Empty ) );
}
sw.WriteLine();
}
}
public int RowCount
{
get
{
return this.Count;
}
}
public int ColCount
{
get
{
return this.maxCol;
}
}
}